This page attempts to show the first uses of various words used in Probability & Statistics. It contains words related to probability & statistics that are extracted from the Earliest Known Uses of Some of the Words of Mathematics pages of Jeff Miller with his permission. Research for his pages is ongoing, and the uses cited in this page should not be assumed to be the first uses that occurred unless it is stated that the term was introduced or coined by the mathematician named. If you are able antedate any of the entries herein, please contact Jeff Miller, a teacher at Gulf High School in New Port Richey, Florida, who maintains these aformentioned pages. See also Jeff Millers Earliest Uses of Various Mathematical Symbols. Texts in red are by Kees Verduin.
In The History of Statistics: The Measurement of Uncertainty before 1900, Stephen M. Stigler writes, "Yule derived what we now, following Fisher, call the analysis of variance breakdown." [James A. Landau]
The form of diagram, however, is much older; there is an example from William Playfair's Commercial and Political Atlas of 1786 at http://www.york.ac.uk/depts/maths/histstat/playfair.gif.
Bar graph is found in 1925 in Statistics by B. F. Young: "Bar-graphs in the form of progress charts are used to represent a changing condition such as the output of a factory" (OED2).
Biased sample is found in 1911 An Introduction to the theory of Statistics by G. U. Yule: "Any sample, taken in the way supposed, is likely to be definitely biassed, in the sense that it will not tend to include, even in the long run, equal proportions of the Aís and [alpha]'s in the original material" (OED2).
Biased sampling is found in F. Yates, "Some examples of biassed sampling," Ann. Eugen. 6 (1935) [James A. Landau].
Central limit theorem appears in the title "Ueber den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung," Math. Z., 15 (1920) by George Polya (1887-1985) [James A. Landau]. Polya apparently coined the term in this paper.
Central limit theorem appears in English in 1937 in Random Variables and Probability Distributions by H. Cramér (David, 1995).
Central tendency is found in 1929 in Kelley & Shen in C. Murchison, Found. Exper. Psychol. 838: "Some investigators have often preferred the median to the mean as a measure of central tendency" (OED2).
Let A and B be two events whose probabilities are (A) and (B). It is understood that the probability (A) is determined without any regard to B when nothing is known about the occurrence or nonoccurrence of B. When it is known that B occurred, A may have a different probability, which we shall denote by the symbol (A, B) and call 'conditional probability of A, given that B has actually happened.'[James A. Landau]
The form of this solution consists in determining certain intervals, which I propose to call the confidence intervals..., in which we may assume are contained the values of the estimated characters of the population, the probability of an error is a statement of this sort being equal to or less than 1 - (epsilon), where (epsilon) is any number 0 < (epsilon) < 1, chosen in advance.
In the modern literature this notion is usually called Fisher-consistency (a name suggested by Rao) to distinguish it from the more standard notion linked to the limiting behavior of a sequence of estimators. The latter is hinted at in Fisher's writings but was perhaps first set out rigorously by Hotelling in the "The Consistency and Ultimate Distribution of Optimum Statistics," Transactions of the American Mathematical Society (1930). [This entry was contributed by John Aldrich, based on David (1995).]
This result enables us to start from the mathematical theory of independent probability as developed in the elementary text books, and build up from it a generalised theory of association, or, as I term it, contingency. We reach the notion of a pure contingency table, in which the order of the sub-groups is of no importance whatever.This citation was provided by James A. Landau.
The term coefficient of correlation was apparently originated by Edgeworth in 1892, according to Karl Pearson's "Notes on the History of Correlation," (reprinted in Pearson & Kendall (1970). It appears in 1892 in F. Y. Edgeworth, "Correlated Averages," Philosophical Magazine, 5th Series, 34, 190-204.
Correlation coefficient appears in a paper published in 1895 [James A. Landau].
The OED2 shows a use of coefficient of correlation in 1896 by Pearson in Proc. R. Soc. LIX. 302: "Let r0 be the coefficient of correlation between parent and offspring." David (1995) gives the 1896 paper by Karl Pearson, "Regression, Heredity, and Panmixia," Phil. Trans. R. Soc., Ser. A. 187, 253-318. This paper introduced the product moment formula for estimating correlations--Galton and Edgeworth had used different methods.
Partial correlation. G. U. Yule introduced "net coefficients" for "coefficients of correlation between any two of the variables while eliminating the effects of variations in the third" in "On the Correlation of Total Pauperism with Proportion of Out-Relief" (in Notes and Memoranda) Economic Journal, Vol. 6, (1896), pp. 613-623. Pearson argued that partial and total are more appropriate than net and gross in Karl Pearson & Alice Lee "On the Distribution of Frequency (Variation and Correlation) of the Barometric Height at Divers Stations," Phil. Trans. R. Soc., Ser. A, 190 (1897), pp. 423-469. Yule went fully partial with his 1907 paper "On the Theory of Correlation for any Number of Variables, Treated by a New System of Notation," Proc. R. Soc. Series A, 79, pp. 182-193.
Multiple correlation. At first multiple correlation referred only to the general approach, e.g. by Yule in Economic Journal (1896). The coefficient arrives later. "On the Theory of Correlation" (J. Royal Statist. Soc., 1897, p. 833) refers to a coefficient of double correlation R1 (the correlation of the first variable with the other two). Yule (1907) discussed the coefficient of n-fold correlation R21(23...n). Pearson used the phrases "coefficient of multiple correlation" in his 1914 "On Certain Errors with Regard to Multiple Correlation Occasionally Made by Those Who Have not Adequately Studied this Subject," Biometrika, 10, pp. 181-187, and "multiple correlation coefficient" in his 1915 paper "On the Partial Correlation Ratio," Proc. R. Soc. Series A, 91, pp. 492-498.
[This entry was largely contributed by John Aldrich.]
Earlier uses of the term covariance are found in mathematics, in a non-statistical sense.
Decile appears in 1882 in Francis Galton, Rep. Brit. Assoc. 1881 245: "The Upper Decile is that which is exceeded by one-tenth of an infinitely large group, and which the remaining nine-tenths fall short of. The Lower Decile is the converse of this" (OED2).
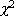 test in the 1922 paper "On
the Interpretation of
test in the 1922 paper "On
the Interpretation of 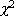 from "Contingency Tables, and the Calculation of P," J.
Royal Statist. Soc., 85, pp. 87-94. He applied the number of
degrees of freedom to distributions related to chi-squared--Student's
distribution and his own z distribution in his 1924 paper, "On
a Distribution Yielding the Error Functions of Several well Known
Statistics," Proceedings of the International Congress of
Mathematics, Toronto, 2, 805-813 [John Aldrich].
from "Contingency Tables, and the Calculation of P," J.
Royal Statist. Soc., 85, pp. 87-94. He applied the number of
degrees of freedom to distributions related to chi-squared--Student's
distribution and his own z distribution in his 1924 paper, "On
a Distribution Yielding the Error Functions of Several well Known
Statistics," Proceedings of the International Congress of
Mathematics, Toronto, 2, 805-813 [John Aldrich].
Dependent variable appears in in 1831 in the second edition of Elements of the Differential Calculus (1836) by John Radford Young: "On account of this dependence of the value of the function upon that of the variable the former, that is y, is called the dependent variable, and the latter, x, the independent variable" [James A. Landau].
Directly proportional is found in 1796 in A Mathematical and Philosophical Dictionary: "Quantities are said to be directly proportional, when the proportion is according to the order of the terms" (OED2).
Direct variation is found in 1856 in Ray's higher arithmetic. The principles of arithmetic, analyzed and practically applied by Joseph Ray (1807-1855):
Variation is a general method of expressing proportion often used, and is either direct or inverse. Direct variation exists between two quantities when they increase togeether, or decrease together. Thus the distance a ship goes at a uniform rate, varies directly as the time it sails; which means that the ratio of any two distances is equal to the ratio of the corresponding times taken in the same order. Inverse variation exists between two quantities when one increases as the other decreases. Thus, the time in which a piece of work will be done, varies inversely as the number of men employed; which means that the ratio of any two times is equal to the ratio of the numbers of men employed for these times, taken in reverse order.This citation was taken from the University of Michigan Digital Library [James A. Landau].
See also W. G. Cochran and C. I. Bliss, "Discriminant functions with covariance," Ann. Math. Statist. 19 (1948) [James A. Landau].
The English term appears in J. L. Doob's "The Limiting Distributions of Certain Statistics," Annals of Mathematical Statistics, 6, (1935), 160-169.
In regression analysis a DUMMY VARIABLE indicates the presence (value 1) or absence of an attribute (0).
A JSTOR search found "dummy variables" for social class and for region in H. S. Houthakker's "The Econometrics of Family Budgets" Journal of the Royal Statistical Society A, 115, (1952), 1-28.
A 1957 article by D. B. Suits, "Use of Dummy Variables in Regression Equations" Journal of the American Statistical Association, 52, 548-551, consolidated both the device and the name.
The International Statistical Institute's Dictionary of Statistical Terms objects to the name: the term is "used, rather laxly, to denote an artificial variable expressing qualitative characteristics .... [The] word 'dummy' should be avoided."
Apparently these variables were not dummy enough for Kendall & Buckland, for whom a dummy variable signifies "a quantity written in a mathematical expression in the form of a variable although it represents a constant", e.g. when the constant in the regression equation is represented as a coefficient times a variable that is always unity.
The indicator device, without the name "dummy variable" or any other, was also used by writers on experiments who put the analysis of variance into the format of the general linear hypothesis, e.g. O. Kempthorne in his Design and Analysis of Experiments (1952) [John Aldrich].
Dorothy Geddes and Sally I. Lipsey, "The Hazards of Sets," The Mathematics Teacher, October 1969 has: "The fact that mathematicians refer to the empty set emphasizes the rather unique nature of this set."
An older term is null set, q. v.
The terms estimation and estimate were introduced in R. A. Fisher's "On the Mathematical Foundations of Theoretical Statistics" (Phil. Trans. R. Soc. 1922). He writes (none too helpfully!): "Problems of estimation are those in which it is required to estimate the value of one or more of the population parameters from a random sample of the population." Fisher uses estimate as a substantive sparingly in the paper.
The phrase unbiassed estimate appears in Fisher's Statistical Methods for Research Workers (1925, p. 54) although the idea is much older.
The expression best linear unbiased estimate appears in 1938 in F. N. David and J. Neyman, "Extension of the Markoff Theorem on Least Squares," Statistical Research Memoirs, 2, 105-116. Previously in his "On the Two Different Aspects of the Representative Method" (Journal of the Royal Statistical Society, 97, 558-625) Neyman had used mathematical expectation estimate for unbiased estimate and best linear estimate for best linear unbiased estimate (David, 1995).
The term estimator was introduced in 1939 in E. J. G. Pitman, "The Estimation of the Location and Scale Parameters of a Continuous Population of any Given Form," Biometrika, 30, 391-421. Pitman (pp. 398 & 403) used the term in a specialised sense: his estimators are estimators of location and scale with natural invariance properties. Now estimator is used in a much wider sense so that Neyman's best linear unbiased estimate would be called a best linear unbiased estimator (David, 1995). [This entry was contributed by John Aldrich.]
Event took on a technical existence when Kolmogorov in the Grundbegriffe der Wahrscheinlichkeitsrechnung (1933) identified "elementary events" ("elementare Ereignisse") with the elements of a collection E (now called the "sample space") and "random events" ("zufällige Ereignisse") with the elements of a set of subsets of E [John Aldrich].
According to Burton (p. 461), the word expectatio first appears in van Schooten's translation of a tract by Huygens.
The two references above point to the same text as Huygens's De
Ratiociniis in Ludo Alae was a translation by van Schooten. NB The word
expectatio is used quite frequently throughout the text.
This is the Latin translation by Van Schooten of the first proposition:
Si a vel b expectem, quorum utriusque aeque facile mihi obtingere possit.
expectatio mea dicenda est (a+b)/2
This is the Dutch text of Huygens'
Van Rekeningh in Spelen van Geluck. This text was published in
1660 but already written in 1656.
Als ick gelijcke kans hebbe om a of b te hebben, dit is my so veel weerdt als (a+b)/2
The litteral translation of the Dutch text is: If I have an equal chance to
get either a or b, this to me is worth as much as (a+b)/2. There is no
explicit mention of expectation only of value, but as the rest of the explanation of the
first proposition is concentrated on the possible outcomes of a game of
chance, expectation is implicitly around.
Expectation appears in English in Browne's 1714 translation of
Huygens's De Ratiociniis in Ludo Alae (David 1995).
This is Browne's 1714 translation of the first proposition:
If I expect a or b, and have an equal chance of gaining either of
them, my Expectation is worth (a+b)/2
See also mathematical expectation.
See also L. H. C. Tippett, "On the extreme individuals and the range of samples taken from a normal population," Biometrika 17 (1925) [James A. Landau].
The term F distribution is found in Leo A. Aroian, "A study of R. A. Fisher's z distribution and the related F distribution," Ann. Math. Statist. 12, 429-448 (1941).
Gaussian distribution and Gaussian law were used by Karl Pearson in 1905 in Biometrika IV: "Many of the other remedies which have been proposed to supplement what I venture to call the universally recognised inadequacy of the Gaussian law .. cannot .. effectively describe the chief deviations from the Gaussian distribution" (OED2).
In an essay in the 1971 book Reconsidering Marijuana, Carl Sagan, using the pseudonym "Mr. X," wrote, "I can remember one occasion, taking a shower with my wife while high, in which I had an idea on the origins and invalidities of racism in terms of gaussian distribution curves. I wrote the curves in soap on the shower wall, and went to write the idea down."
The term was also used by Aristotle.
According to the Catholic Encyclopedia, the word harmonic first appears in a work on conics by Philippe de la Hire (1640-1718) published in 1685.
Harmonical mean is found in English in the 1828 Webster dictionary:
Harmonical mean, in arithmetic and algebra, a term used to express certain relations of numbers and quantities, which are supposed to bear an analogy to musical consonances.Harmonic mean is found in 1851 in Problems in illustration of the principles of plane coordinate geometry by William Walton [University of Michigan Digital Library].
Harmonic mean is also found in 1851 in The principles of the solution of the Senate-house 'riders,' exemplified by the solution of those proposed in the earlier parts of the examinations of the years 1848-1851 by Francis James Jameson: "Prove that the discount on a sum of money is half the harmonic mean between the principal and the interest" [University of Michigan Digital Library].
Many authors prefer the spelling heteroskedasticity. J. Huston McCulloch (Econometrica 1985) discusses the linguistic aspects and decides for the k-spelling. Pearson recalled that when he set up Biometrika in 1901 Edgeworth had insisted the name be spelled with a k. By 1932 when Econometrica was founded standards had fallen or tastes had changed. [This entry was contributed by John Aldrich, referring to OED2 and David, 1995.]
In Philos. Trans. R. Soc. A. CLXXXVI, (1895) 399 Pearson explained that term was "introduced by the writer in his lectures on statistics as a term for a common form of graphical representation, i.e., by columns marking as areas the frequency corresponding to the range of their base."
S. M. Stigler writes in his History of Statistics that Pearson used the term in his 1892 lectures on the geometry of statistics.
The earliest citation in the OED2 is in 1891 in E. S. Pearson Karl Pearson (1938).
According to Heinz Lueneburg, the term numero sano "was used extensively by Luca Pacioli in his Summa. Before Pacioli, it was already used by Piero della Francesca in his Trattato d'abaco. I also find it in the second edition of Pietro Cataneo's Le pratiche delle due prime matematiche of 1567. I haven't seen the first edition. Counting also Fibonacci's Latin numerus sanus, the word sano was used for at least 350 years to denote an integral (untouched, virginal) number. Besides the words sanus, sano, the words integer, intero, intiero were also used during that time."
The first citation for whole number in the OED2 is from about 1430 in Art of Nombryng ix. EETS 1922:
Of nombres one is lyneal, ano(th)er superficialle, ano(th)er quadrat, ano(th)cubike or hoole.In the above quotation (th) represents a thorn. In this use, whole number has the obsolete definition of "a number composed of three prime factors," according to the OED2.
Whole number is found in its modern sense in the title of one of the earliest and most popular arithmetics in the English language, which appeared in 1537 at St. Albans. The work is anonymous, and its long title runs as follows: "An Introduction for to lerne to reken with the Pen and with the Counters, after the true cast of arismetyke or awgrym in hole numbers, and also in broken" (Julio González Cabillón).
Oresme used intégral.
Integer was used as a noun in English in 1571 by Thomas Digges (1546?-1595) in A geometrical practise named Pantometria: "The containing circles Semidimetient being very nighe 11 19/21 for exactly nether by integer nor fraction it can be expressed" (OED2).
Integral number appears in 1658 in Phillips: "In Arithmetick integral numbers are opposed to fraction[s]" (OED2).
Whole number is most frequently defined as Z+, although it is sometimes defined as Z. In Elements of the Integral Calculus (1839) by J. R. Young, the author refers to "a whole number or 0" but later refers to "a positive whole number."
See also W. Feller, "On the Kolmogorow-Smirnov limit theorems for empirical distributions," Ann. Math. Statist. 19 (1948) [James A. Landau].
Latin square appears in English in 1890 in the title of a paper by Arthur Cayley, "On Latin Squares" in Messenger of Mathematics.
The term was introduced into statistics by R. A. Fisher, according to Tankard (p. 112). Fisher used the term in 1925 in Statistical Methods Res. Workers (OED2).
Graeco-Latin square appears in 1934 in R. A. Fisher and F. Yates, "The 6 x 6 Latin Squares," Proceedings of the Cambridge Philosophical Society 30, 492-507.
According to Porter (p. 12), Poisson coined the term in 1835.
Formerly, likelihood was a synonym for probability, as it still is in everyday English. (See the entry on maximum likelihood and the passage quoted there for Fisher's attempt to distinguish the two. In 1921 Fisher referred to the value that maximizes the likelihood as "the optimum.")
Likelihood first appeared in a Bayesian context in H. Jeffreys's Theory of Probability (1939) [John Aldrich, based on David (2001)].
The principle (without a name) can be traced back to R. A. Fisher's writings of the 1920s though its clearest earlier manifestation is in Barnard's 1949 "Statistical Inference" (Journal of the Royal Statistical Society. Series B, 11, 115-149). On these earlier outings the principle attracted little attention.
The standing of "likelihood ratio" was confirmed by S. S. Wilks's "The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses," Annals of Mathematical Statistics, 9, (1938), 60-620 [John Aldrich, based on David (2001)].
See also expectation.
The solution of the problems of calculating from a sample the parameters of the hypothetical population, which we have put forward in the method of maximum likelihood, consists, then, simply of choosing such values of these parameters as have the maximum likelihood. Formally, therefore, it resembles the calculation of the mode of an inverse frequency distribution. This resemblance is quite superficial: if the scale of measurement of the hypothetical quantity be altered, the mode must change its position, and can be brought to have any value, by an appropriate change of scale; but the optimum, as the position of maximum likelihood may be called, is entirely unchanged by any such transformation. Likelihood also differs from probability in that it is not a differential element, and is incapable of being integrated: it is assigned to a particular point of the range of variation, not to a particular element of it.
In 1571, A geometrical practise named Pantometria by Thomas Digges (1546?-1595) has: "When foure magnitudes are...in continual proportion, the first and the fourth are the extremes, and the second and thirde the meanes" (OED2).
Mean is found in 1755 in Thomas Simpson, "An ATTEMPT to shew the Advantage, arising by Taking the Mean of a Number of Observations, in practical Astronomy," Philosophical Transactions of the Royal Society of London.
Mean error is found in 1853 in A dictionary of arts, manufactures, and mines; containing a clear exposition of their principles and practice by Andrew Ure [University of Michigan Digital Library].
Mean error is found in English in an 1857 translation of Gauss's Theoria motus: Consequently, if we desire the greatest accuracy, it will be necessary to compute the geocentric place from the elements for the same time, and afterwards to free it from the mean error A, in order that the most accurate position may be obtained. But it will in general be abundantly sufficient if the mean error is referred to the observation nearest to the mean time" [University of Michigan Digital Library].
In 1894 in Phil. Trans. Roy. Soc, Karl Pearson has "error of mean square" as an alternate term for "standard-deviation" (OED2).
In Higher Mathematics for Students of Chemistry and Physics (1912), J. W. Mellor writes:
In Germany, the favourite method is to employ the mean error, which is defined as the error whose square is the mean of the squares of all the errors, or the "error which, if it alone were assumed in all the observations indifferently, would give the same sum of the squares of the errors as that which actually exists." ...In a footnote, Mellor writes, "Some writers call our "average error" the "mean error," and our "mean error" the "error of mean square" [James A. Landau].The mean error must not be confused with the "mean of the errors," or, as it is sometimes called, the average error, another standard of comparison defined as the mean of all the errors regardless of sign.
Median was used in English by Francis Galton in Report of the British Association for the Advancement of Science in 1881: "The Median, in height, weight, or any other attribute, is the value which is exceeded by one-half of an infinitely large group, and which the other half fall short of" (OED2).
"Minimum" and "small" were the early English translations of moindres (David, 1995).
Method of least squares occurs in English in 1825 in the title "On the Method of Least Squares" by J. Ivory in Philosophical Magazine, 65, 3-10.
Modulus (a coefficient that expresses the degree to which a
body possesses a particular property) appears in the 1738 edition of
The Doctrine of Chances: or, a Method of Calculating the
Probability of Events in Play by Abraham De Moivre (1667-1754)
[James A. Landau].
See also Stigler (1986), page 83.
The Egyptologist Flinders Petrie (1883) refers to the modulus as a measure
of dispersion. His sources are Airy's Theory of Errors (18752)
and De Morgan's Essay on Probability (1838). The modulus equals
÷2 s. FY Edgeworth also uses the modulus in 1885.
(Corollary 6)...To apply this to particular Examples, it will be necessary to estimate
the frequency of an Event's happening or failing by the Square-root of
the number which denotes how many Experiments have been, or are designed
to be taken, and this Square-root, according as at has been already
hinted at in the fourth Corollary, will be as it were the Modulus by
which we are to regulate our Estimation, and therefore suppose the
number of Experiments to be taken is 3600, and that it were required to
assign the Probability of the Event's neither happening oftner than 2850
times, nor more rarely than 1750, which two numbers may be varied at
pleasure, provided they he equally distant from the middle Sum 1800, then
make the half difference between the two numbers 1850 and 1750, that
is, in this case, 50=s÷n; now having supposed 3600=n, then
÷n will be 60, which will make it that 50 will be =60s, and
consequently s=50/60=5/6, and therefore if we take the
proportion, which in an infinite power, the double Sum of the Terms
corresponding to the Interval 5/6 ÷n, bears to the Sum of
all the Terms, we shall have the Probability required exceeding near.
Modulus (in number theory) was introduced by Gauss in 1801 in Disquisitiones arithmeticae:
Si numerus a numerorum b, c differentiam metitur, b et c secundum a congrui dicuntur, sin minus, incongrui; ipsum a modulum appelamus. Uterque numerorum b, c priori in casu alterius residuum, in posteriori vero nonresiduum vocatur. [If a number a measure the difference between two numbers b and c, b and c are said to be congruent with respect to a, if not, incongruent; a is called the modulus, and each of the numbers b and c the residue of the other in the first case, the non-residue in the latter case.]Modulus (in number theory) is found in English in 1811 in An Elementary Investigation of the Theory of Numbers by Peter Barlow [James A. Landau].
Modulus (the length of the vector a + bi) is due to Jean Robert Argand (1768-1822) (Cajori 1919, page 265). The term was first used by him in 1814, according to William F. White in A Scrap-Book of Elementary Mathematics (1908).
Modulus for ÷(a2 + b2) was used by Augustin-Louis Cauchy (1789-1857) in 1821.
Moment appears in English in the obsolete sense of "momentum" in 1706 in Synopsis Palmariorum Matheseos by William Jones: "Moment..is compounded of Velocity..and..Weight" (OED2).
Moment of a force appears in 1830 in A Treatise on Mechanics by Henry Kater and Dionysius Lardner (OED2).
Moment was used in a statistics sense by Karl Pearson in October 1893 in Nature: "Now the centre of gravity of the observation curve is found at once, also its area and its first four moments by easy calculation" (OED2).
The phrase method of moments was used in a statistics sense in the first of Karl Pearson's "Contributions to the Mathematical Theory of Evolution" (Phil. Trans. R. Soc. 1894). The method was used to estimate the parameters of a mixture of normal distributions. For several years Pearson used the method on different problems but the name only gained general currency with the publication of his 1902 Biometrika paper "On the systematic fitting of curves to observations and measurements" (David 1995). In "On the Mathematical Foundations of Theoretical Statistics" (Phil. Trans. R. Soc. 1922), Fisher criticized the method for being inefficient compared to his own maximum likelihood method (Hald pp. 650 and 719). [This paragraph was contributed by John Aldrich.]
According to W. L. Winston, the term was coined by Ulam and von Neumann in the feasibility project of atomic bomb by simulations of nuclear fission; they gave the code name Monte Carlo for these simulations.
According to several Internet web pages, the term was coined in 1947 by Nicholas Metropolis, inspired by Ulam's interest in poker during the Manhattan Project of World War II.
Monte Carlo method occurs in the title "The Monte Carlo Method" by Nicholas Metropolis in the Journal of the American Statistical Association 44 (1949).
Monte Carlo method also appears in 1949 in Math. Tables & Other Aids to Computation III: "This method of solution of problems in mathematical physics by sampling techniques based on random walk models constitutes what is known as the 'Monte Carlo' method. The method as well as the name for it were apparently first suggested by John von Neumann and S. M. Ulam" (OED2).
Normal probability curve was used by Karl Pearson (1857-1936) in 1893 in Nature 26 Oct. 615/2: "As verification note that for the normal probability curve 3µ22 = µ4 and µ3 = 0" (OED2).
Pearson used normal curve in 1894 in "Contributions to the Mathematical Theory of Evolution":
When a series of measurements gives rise to a normal curve, we may probably assume something approaching a stable condition; there is production and destruction impartially around the mean.The above quotation is from Porter.
Pearson used normal curve in 1894 in Phil. Trans. R. Soc. A. CLXXXV. 72: "A frequency-curve, which for practical purposes, can be represented by the error curve, will for the remainder of this paper be termed a normal curve."
Normal distribution appears in 1897 in Proc. R. Soc. LXII. 176: "A random selection from a normal distribution" (OED2).
According to Hald, p. 356:
The new error distribution was first of all called the law of error, but many other names came to be used, such as the law of facility of errors, the law of frequency of errors, the Gaussian law of errors, the exponential law, and the typical law of errors. In his paper "Typical laws of heredity" Galton (1877) studied biological variation, and he therefore replaced the term "error" with "deviation," and referring to Quetelet, he called the distribution "the mathematical law of deviation." Chapter 5 in Galton's Natural Inheritance (1889a) is entitled "Normal Variability," and he writes consistently about "The Normal Curve of Distributions," an expression that caught on.According to Walker (p. 185), Karl Pearson did not coin the term normal curve. She writes, "Galton used it, as did also Lexis, and the writer has not found any reference which seems to be its first use."
Nevertheless, "...Pearson's consistent and exclusive use of this term in his epoch-making publications led to its adoption throughout the statistical community" (DSB).
However, Porter (p. 312) calls normal curve a "Pearsonian neologism."
The "null hypothesis" is often identified with the "hypothesis tested" of J. Neyman and E. S. Pearson's 1933 paper, "On the Problems of the Most Efficient Tests of Statistical Hypotheses" Phil. Trans. Roy. Soc. A (1933), 289-337, and represented by their symbol H0. Neyman did not like the "null hypothesis," arguing (First Course in Probability and Statistics, 1950, p. 259) that "the original term 'hypothesis tested' seems more descriptive." It is not clear, however, that "hypothesis tested" was ever floated as a technical term [John Aldrich].
Parameter is found in 1922 in R. A. Fisher, "On the Mathematical Foundations of Theoretical Statistics," Philosoophical Transactions of the Royal Society of London, Ser. A. 222, 309-368 (David, 1995).
The term was introduced by Fisher, according to Hald, p. 716.
According to Hald (p. 604), Galton introduced the term.
Earlier, Leibniz had used the term variationes and Wallis had adopted alternationes (Smith vol. 2, page 528).
Poisson distribution appears in 1922 in Ann. Appl. Biol. IX. 331: "When the statistical examination of these data was commenced it was not anticipated that any clear relationship with the Poisson distribution would be obtained" (OED2).
As, if any one shou'd lay that he wou'd throw the Number 6 with a single die the first throw, it is indeed uncertain whether he will win or lose; but how much more probability there is that he shou'd lose than win, is easily determin'd, and easily calculated.This is from the Latin translation by van Schooten of Huygens' introduction:
Ut si quis primo jactu una tessera senarium jacerere contendat, incertum quidem an vincet; at quanto verisimilius sit eum perdere quam vincere, reipsa definitum est, calculoque subducitur.This is the Dutch text of the introduction of Huygens' Van Rekeningh in Spelen van Geluck. This text was published in 1660 but allready written in 1656.
Als, by exempel. Die met een dobbel-stee(n) ten eerste(n) een ses neemt te werpen / het is onseecker of hy het winnen sal of niet; maer hoe veel minder kans hy heeft om te winnen als om te verliesen / dat is in sich selven seecker / en werdt door reeckeningh uyt-gevonden.and
TO resolve which, we must observe, First, That there are six several Throws upon one Die, which all have an equal probability of coming up.This is from the Latin translation by van Schooten of Huygens' 9th proposition:
Ad quas solvendas advertendum est. Primo unius tesserae sex esse jactus diversos, quorum quivis aeque facile eveniat.This is the Dutch text from the 9th proposition of Huygens' Van Rekeningh in Spelen van Geluck.
Om welcke te solveeren / so moet hier op worden acht genomen. Eerstelijck dat op 1 steen zijn 6 verscheyde werpen / die even licht konnen gebeuren.Although Huygens uses the word Kans (Chance) repeatedly in his Dutch text, van Schooten seems in his Latin translation to rephrase the text every time just to circumvent the use of a single term for probability. (See p. 11-13, in Waerden, BL van der (ed, 1975) Die Werke von Jacob Bernoulli, Band 3, Birckhauser Verlag Basel) The opening sentence of De Mensura Sortis (1712) by Abraham de Moivre (1667-1754) is translated:
If p is the number of chances by which a certain event may happen, and q is the number of chances by which it may fail; the happenings as much as the failings have their degree of probability: But if all the chances by which the event may happen or fail were equally easy; the probability of happening will be to the probability of failing as p to q.The first citation for probability in the OED2 is in 1718 in the title The Doctrine of Chances: or, a Method of Calculating the Probability of Events in Play by De Moivre.
Pascal did not use the term (DSB).
Wahrscheinlichkeitsdichte appears in 1912 in Wahrscheinlichkeitsrechnung by A. A. Markoff (David, 1998).
In J. V. Uspensky, Introduction to Mathematical Probability (1937), page 264 reads "The case of continuous F(t), having a continuous derivative f(t) (save for a finite set of points of discontinuity), corresponds to a continuous variable distributed with the density f(t), since F(t) = integral from -infinity to t f(x)dx" [James A. Landau].
Probability density appears in 1939 in H. Jeffreys, Theory of Probability: "We shall usually write this briefly P(dx|p) = f'(x)dx, dx on the left meaning the proposition that x lies in a particular range dx. f'(x) is called the probability density" (OED2).
Probability density function appears in 1946 in an English translation of Mathematical Methods of Statistics by Harald Cramér. The original appeared in Swedish in 1945 [James A. Landau].
According to Hald (p. 360), Friedrich Wilhelm Bessel (1784-1846)
introduced the term probable error (wahrscheinliche
Fehler) without detailed explanation in 1815 in "Ueber den Ort
des Polarsterns" in Astronomische Jahrbuch für das Jahr
1818, and in 1816 defined the term in "Untersuchungen über
die Bahn des Olbersschen Kometen" in Abh. Math. Kl. Kgl. Akad.
Wiss., Berlin. Bessel used the term for the 50% interval around
the least-squares estimate. All calculations and constants
related to the probable error and starting with Gauss are based on the
assumption that the errors follow a normal distribution. A modern
approximation of the ratio r/E2 is
0.674489749382381
Also in 1816 Gauss published a paper Bestimmung der
Genauigkeit der Beobachtungen in which he showed several methods to
calculate the Probable Error. He wrote:"... wir wollen diese Grösse
... der wahrscheinleichen Fehler nennen, und ihn met r bezeichnen."
His calculations were based on a general dispersion measure Ek=
(S(dk)/n)1/k. Gauss showed that
k = 2 results in the most precise value of the probable error: r =
0.6744897 * E2. Notice that E2 is the mean error
(i.e. the sample standard deviation).
Probable error is found in 1852 in Report made to the Hon. Thomas Corwin, secretary of the treasury by Richard Sears McCulloh. This book uses the term four times, but on the one occasion where a computation can be seen the writer takes two measurements and refers to the difference between them as the "probable error" [University of Michigan Digital Library].
Probable error is found in 1853 in A dictionary of science, literature & art edited by William Thomas Brande: "... the probable error is the quantity, which is such that there is the same probability of the difference between the determination and the true absolute value of the thing to be determined exceeding or falling short of it. Thus, if twenty measurements of an angle have been made with the theodolite, and the arithmetical mean or average of the whole gives 50° 27' 13"; and if it be an equal wager that the error of this result (either in excess or defect) is less than two seconds, or greater than two seconds, then the probable error of the determination is two seconds" [University of Michigan Digital Library].
Probable error is found in 1853 in
A collection of tables and fromulae (=formulae) useful in surveying, geodesy, and practical astronomy
by Thomas Jefferson Lee. The term is defined,
in modern terminology, as the sample standard deviation times .674489 divided by the square
root of the number of observations
[James A. Landau; University of Michigan Digital Library].
Actually on page 238 of the book mentioned above T.J. Lee
presents two versions of the probable error: r and R. The one called r is
the PE of a single observation with r = 0.674489 * E2 with
E2 = s and the one called R is the PE
of final result (ie of the mean) with R = r / ÷n.
Probable error is found in 1855 in A treatise on land surveying by William Mitchell Gillespie: "When a number of separate observations of an angle have been made, the mean or average of them all, (obtained by dividing the sum of the readings by their number,) is taken as the true reading. The 'Probable error' of this mean, is the quantity, (minutes or seconds) which is such that there is an even chance of the real error being more or less than it. Thus, if ten measurements of an angle gave a mean of 350 18', and it was an equal wager that the error of this result, too much or too little, was half a minute, then half a minute would be the 'Probable error' of this determination. This probable error is equal to the square root of the sum of the squares of the errors (i. e. the differences of each observation from the mean) divided by the number of observations, and multiplied by the decimal 0.674489. The same result would be obtained by using what is called 'The weight' of the observation. It is equal to the square of the number of observations divided by twice the sum of the squares of the errors. The 'Probable error' is equal to 0.476936 divided by the square root of the weight" [University of Michigan Digital Library].
Probable error is found in 1865 in Spherical astronomy by Franz Brünnow (an English translation by the author of the second German edition): "In any series of errors written in the order of their absolute magnitude and each written as often as it actually occurs, we call that error which stands exactly in the middle, the probable error" [University of Michigan Digital Library].
In 1872 Elem. Nat. Philos. by Thomson & Tait has: "The probable error of the sum or difference of two quantities, affected by independent errors, is the square root of the sum of the squares of their separate probable errors" (OED2).
In 1889 in Natural Inheritance, Galton criticized the term probable error, saying the term was "absurd" and "quite misleading" because it does not refer to what it seems to, the most probable error, which would be zero. He suggested the term Probability Deviation be substituted, opening the way for Pearson to introduce the term standard deviation (Tankard, p. 48).
Higher and lower quartile are found in 1879 in D. McAlister, Proc. R. Soc. XXIX: "As these two measures, with the mean, divide the curve of facility into four equal parts, I propose to call them the 'higher quartile' and the 'lower quartile' respectively. It will be seen that they correspond to the ill-named 'probable errors' of the ordinary theory" (OED2).
Upper and lower quartile appear in 1882 in F. Galton, "Report of the Anthropometric Committee," Report of the 51st Meeting of the British Association for the Advancement of Science, 1881, p. 245-260 (David, 1995).
See also L. H. C. Tippett, "Random Sampling Numbers 1927," Tracts for Computers, No. 15 (1927) [James A. Landau].
Random choice appears in the Century Dictionary (1889-1897).
Random selection occurs in 1897 in Proc. R. Soc. LXII. 176: "A random selection from a normal distribution" (OED2).
Random sampling was used by Karl Pearson in 1900 in the title, "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling," Philosophical Magazine 50, 157-175 (OED2).
Random sample is found in 1903 in Biometrika II. 273: "If the whole of a population were taken we should have certain values for its statistical constants, but in actual practice we are only able to take a sample, which should if possible be a random sample" (OED2).
Random variable is found in 1934 in A. Winter, "On Analytic Convolutions of Bernoulli Distributions," American Journal of Mathematics, 56, 659-663 (David, 1998).
According to Tankard (p. 112), R. A. Fisher "may ... have coined the term randomization; at any rate, he certainly gave it the important position in statistics that it has today."
Rank correlation appears in 1907 in Drapers' Company Res. Mem. (Biometric Ser.) IV. 25: "No two rank correlations are in the least reliable or comparable unless we assume that the frequency distributions are of the same general character .. provided by the hypothesis of normal distribution. ... Dr. Spearman has suggested that rank in a series should be the character correlated, but he has not taken this rank correlation as merely the stepping stone..to reach the true correlation" (OED2).
Porter (page 289), referring to Galton, writes:
He did, however, change his terminology from "reversion" to "regression," a shift whose significance is not entirely clear. Possibly he simply felt that the latter term expressed more accurately the fact that offspring returned only part way to the mean. More likely, the change reflected his new conviction, first expressed in the same papers in which he introduced the term "regression," that this return to the mean reflected an inherent stability of type, and not merely the reappearance of remote ancestral gemmules.In 1859 Charles Darwin used reversion in a biological context in The Origin of Species (1860): "We could not have told, whether these characters in our domestic breeds were reversions or only analogous variations" (OED2).
Galton used the term reversion coefficient in "Typical laws of heredity," Nature 15 (1877), 492-495, 512-514 and 532-533 = Proceedings of the Royal Institution of Great Britain 8 (1877) 282-301.
Galton used regression in a genetics context in "Section H. Anthropology. Opening Address by Francis Galton," Nature, 32, 507-510 (David, 1995).
Galton also used law of regression in 1885, perhaps in the same address.
Karl Pearson used regression and coefficient of regression in 1897 in Phil. Trans. R. Soc.:
The coefficient of regression may be defined as the ratio of the mean deviation of the fraternity from the mean off-spring to the deviation of the parentage from the mean parent. ... From this special definition of regression in relation to parents and offspring, we may pass to a general conception of regression. Let A and B be two correlated organs (variables or measurable characteristics) in the same or different individuals, and let the sub-group of organs B, corresponding to a sub-group of A with a definite value a, be extracted. Let the first of these sub-groups be termed an array, and the second a type. Then we define the coefficient of regression of the array on the type to be the ratio of the mean-deviation of the array from the mean B-organ to the deviation of the type a from the mean A-organ.[OED2]
The phrase "multiple regression coefficients" appears in the 1903 Biometrika paper "The Law of Ancestral Heredity" by Karl Pearson, G. U. Yule, Norman Blanchard, and Alice Lee. From around 1895 Pearson and Yule had worked on multiple regression and the phrase "double regression" appears in Pearson's paper "Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity, and Panmixia" (Phil. Trans. R. Soc. 1896). [This paragraph was contributed by John Aldrich.]
The term may have been used earlier by Richard von Mises (1883-1953).
Scattergram is found in 1938 in A. E. Waugh, Elem. Statistical Method: "This is the method of plotting the data on a scatter diagram, or scattergram, in order that one may see the relationship" (OED2).
Scatterplot is found in 1939 in Statistical Dictionary of Terms and Symbols by Kurtz and Edgerton (David, 1998).
In 1946 - still in the genetic context - Fisher ("A System of Scoring Linkage Data, with Special Reference to the Pied Factors in Mice. Amer. Nat., 80: 568-578) described an iterative method for obtaining the maximum likelihood value. Rao's 1948 J. Roy. Statist. Soc. B paper treats the method in a more general framework and the phrase "Fisher's method of scoring" appears in a comment by Hartley. Fisher had already used the method in a general context in his 1925 "Theory of Statistical Estimation" paper (Proc. Cambr. Philos. Soc. 22: 700-725) but it attracted neither attention nor name. [This entry was contributed by John Aldrich, with some information taken from David (1995).]
Menge (set) is found in Geometrie der Lage (2nd ed., 1856) by Carl Georg Christian von Staudt: "Wenn man die Menge aller in einem und demselben reellen einfoermigen Gebilde enthaltenen reellen Elemente durch n + 1 bezeichnet und mit diesem Ausdrucke, welcher dieselbe Bedeutung auch in den acht folgenden Nummern hat, wie mit einer endlichen Zahl verfaehrt, so ..." [Ken Pledger].
Georg Cantor (1845-1918) did not define the concept of a set in his early works on set theory, according to Walter Purkert in Cantor's Philosophical Views.
Cantor's first definition of a set appears in an 1883 paper: "By a set I understand every multitude which can be conceived as an entity, that is every embodiment [Inbegriff] of defined elements which can be joined into an entirety by a rule." This quotation is taken from ‹ber unendliche lineare Punctmannichfaltigkeiten, Mathematische Annalen, 21 (1883).
In 1895 Cantor used the word Menge in Beiträge zur Begründung der Transfiniten Mengenlehre, Mathematische Annalen, 46 (1895):
By a set we understand every collection [Zusammenfassung] M of defined, well-distinguished objects m of our intuition [Zusammenfassung] or our thinking (which are called the elements of M brought together to form an entirety.This translation was taken from Cantor's Philosophical Views by Walter Purkett.
Significance is found in 1888 in Logic of Chance by John Venn: "As before, common sense would feel little doubt that such a difference was significant, but it could give no numerical estimate of the significance" (OED2).
Test of significance and significance test are found in 1907 in Biometrika V. 183: " Several other cases of probable error tests of significance deserve reconsideration" (OED2).
Testing the significance is found in "New tables for testing the significance of observations," Metron 5 (3) pp 105-108 (1925) [James A. Landau].
Statistically significant is found in 1931 in L. H. C. Tippett, Methods Statistics: "It is conventional to regard all deviations greater than those with probabilities of 0.05 as real, or statistically significant" (OED2).
Statistical significance is found in 1938 in Journal of Parapsychology: "The primary requirement of statistical significance is met by the results of this investigation" (OED2).
See also rank correlation.
A quantity of bones are taken from an ossuarium, and are put together in groups which are asserted to be those of individual skeletons. To test this a biologist takes the triplet femur, tibia, humerus, and seeks the correlation between the indices femur/humerus and tibia/humerus. He might reasonably conclude that this correlation marked organic relationship, and believe that the bones had really been put together substantially in their individual grouping. As a matter of fact ... there would be ... a correlation of about 0.4 to 0.5 between these indices had the bones been sorted absolutely at random.The term has been applied to other correlation scenarios with potential for misleading inferences. In Student's "The Elimination of Spurious Correlation due to Position in Time or Space" (Biometrika, 10, (1914), 179-180) the source of the spurious correlation is the common trends in the series. In H. A. Simon's "Spurious Correlation: A Causal Interpretation," Journal of the American Statistical Association, 49, (1954), pp. 467-479 the source of the spurious correlation is a common cause acting on the variables. In the recent spurious regression literature in time series econometrics (Granger & Newbold, Journal of Econometrics, 1974) the misleading inference comes about through applying the correlation theory for stationary series to non-stationary series. The dangers of doing this were pointed out by G. U. Yule in his 1926 "Why Do We Sometimes Get Nonsense Correlations between Time-series? A Study in Sampling and the Nature of Time-series," Journal of the Royal Statistical Society, 89, 1-69. (Based on Aldrich 1995)
The term "standard deviation" was introduced in a lecture of 31 January, 1893, as a convenient substitute for the cumbersome "root mean square error" and the older expressions "error of mean square" and "mean error."The OED2 shows a use of standard deviation in 1894 by Pearson in "Contributions to the Mathematical Theory of Evolution, Philosophical Transactions of the Royal Society of London, Ser. A. 185, 71-110: "Then s will be termed its standard-deviation (error of mean square)."
Standard score is dated 1928 in MWCD10.
The earliest citation in the OED2 is from the Baltimore Sun, Oct. 1, 1945, "The result .. was a 'stanine' rating (stanine being an invented word, from 'standard of nine')."
Stanines were first used to describe an examinee's performance on a battery of tests constructed for the U. S. Army Air Force during World War II.
This term was introduced in 1922 by Fisher, according to Tankard (p. 112).
The term statistic was not well-received initially. Arne Fisher (no relation) asked Fisher, "Where ... did you get that atrocity, a statistic? (letter (p. 312) in J. H. Bennet Statistical Inference and Analysis: Selected Correspondence of R. A. Fisher (1990).) Karl Pearson objected, "Are we also to introduce the words a mathematic, a physic, an electric etc., for parameters or constants of other branches of science?" (p. 49n of Biometrika, 28, 34-59 1936). [These two quotations were provided by John Aldrich.]
In Webster's dictionary of 1828 the definition of statistics is: "A collection of facts respecting the state of society, the condition of the people in a nation or country, their health, longevity, domestic economy, arts, property and political strength, the state of the country, &c."
In its modern sense, the term was used in 1917 by Ladislaus Josephowitsch Bortkiewicz (1868-1931) in Die Iterationem 3: "Die an der Wahrscheinlichkeitstheorie orientierte, somit auf 'das Gesetz der Grossen Zahlen' sich gründende Betrachtng empirischer Vielheiten mö ge als Stochastik ... bezeichnet werden" (OED2).
Stochastic process is found in A. N. Kolmogorov, "Sulla forma generale di un prozesso stocastico omogeneo," Rend. Accad. Lincei Cl. Sci. Fis. Mat. 15 (1) page 805 (1932) [James A. Landau].
Stochastic process is also found in A. Khintchine "Korrelationstheorie der stationäre stochastischen Prozesse," Math. Ann. 109 (1934) [James A. Landau].
Stochastic process occurs in English in "Stochastic processes and statistics," Proc. Natl. Acad. Sci. USA 20 (1934).
In his 1908 paper, "The Probable Error of a Mean," Biometrika 6, 1-25 Gosset introduced the statistic, z, for testing hypotheses on the mean of the normal distribution. Gosset used the divisor n, not the modern (n - 1), when he estimated s and his z is proportional to t with t = z ÷(n - 1). Fisher introduced the t form for it fitted in with his theory of degrees of freedom. Fisher's treatment of the distributions based on the normal distribution and the role of degrees of freedom was given in "On a Distribution Yielding the Error Functions of Several well Known Statistics," Proceedings of the International Congress of Mathematics, Toronto, 2, 805-813. The t symbol appears in this paper but although the paper was presented in 1924, it was not published until 1928 (Tankard, page 103; David, 1995). According to the OED2, the letter t was chosen arbitrarily. A new symbol suited Fisher for he was already using z for a statistic of his own (see entry for F).
Student's distribution (without "t") appears in 1925 in R. A. Fisher, "Applications of 'Student's' Distribution," Metron 5, 90-104 and in Statistical Methods for Research Workers (1925). The book made Student's distribution famous; it presented new uses for the tables and made the tables generally available.
"Student's" t-distribution appears in 1929 in Nature (OED2).
t-distribution appears (without Student) in A. T. McKay, "Distribution of the coefficient of variation and the extended 't' distribution," J. Roy. Stat. Soc., n. Ser. 95 (1932).
t-test is found in 1932 in R. A. Fisher, Statistical Methods for Research Workers: "The validity of the t-test, as a test of this hypothesis, is therefore absolute" (OED2).
Eisenhart (1979) is the best reference for the evolution of t, although Tankard and Hald also discuss it.
[This entry was largely contributed by John Aldrich.]
Studentized D2 statistic is found in R. C. Bose and S. N. Roy, "The exact distribution of the Studentized D2 statistic," Sankhya 3 pt. 4 (1935) [James A. Landau].
The statistic chosen should summarise the whole of the relevant information supplied by the sample. This may be called the Criterion of Sufficiency. ... In the case of the normal curve of distribution it is evident that the second moment is a sufficient statistic for estimating the standard deviation.According to Hald (page 452), Fisher introduced the term sufficiency in a 1922 paper.
Errors of first and second kind is found in 1933 in J. Neyman and E. S. Pearson, "On the Problems of the Most Efficient Tests of Statistical Hypotheses," Philosophical Transactions of the Royal Society of London, Ser. A (1933), 289-337 (David, 1995).
Type I error and Type II error are found in 1933 in J. Neyman and E. S. Pearson, "The Testing of Statistical Hypotheses in Relation to Probabilities A Priori," Proceedings of the Cambridge Philosophical Society, 24, 492-510 (David, 1995).
Uniformly distributed is found in H. Sakamoto, "On the distributions of the product and the quotient of the independent and uniformly distributed random variables," Tohoku Math. J. 49 (1943).
Variance was introduced by Ronald Aylmer Fisher in 1918 in "The Correlation Between Relatives on the Supposition of Mendelian Inheritance," Transactions of the Royal Society of Edinburgh, 52, 399-433: "It is ... desirable in analysing the causes of variability to deal with the square of the standard deviation as the measure of variability. We shall term this quantity the Variance."
Euler's system of notation appears in 1863 in An outline of the necessary laws of thought: a treatise on pure and applied logic by William Thomson (University of Michigan Digital Library).
Euler's notation appears in about 1869 in The principles of logic, for high schools and colleges by Aaron Schuyler (University of Michigan Digital Library).
Euler's diagram appears in 1884 in Elementary Lessons in Logic by W. Stanley Jevons: "Euler's diagram for this proposition may be constructed in the same manner as for the proposition I as follows:..."
Euler's circles appears in 1893 in Logic by William Minto (1845-1893): "The relations between the terms in the four forms are represented by simple diagrams known as Euler's circles."
Euler's circles appears in October 1937 in George W. Hartmann, "Gestalt Psychology and Mathematical Insight," The Mathematics Teacher: "But in the case of 'Euler's circles' as used in elementary demonstrations of formal logic, one literally 'sees' how intimately syllogistic proof is linked to direct sensory perception of the basic pattern. It seems that the famous Swiss mathematician of the eighteenth century was once a tutor by correspondence to a dull-witted Russian princess and devised this method of convincing her of the reality and necessity of certain relations established deductively."
Venn diagram appears in 1918 in A Survey of Symbolic Logic by Clarence Irving Lewis: "This method resembles nothing so much as solution by means of the Venn diagrams" (OED2).